Vectors & Scalars

A scalar is a quantity that has magnitude only.

e.g. mass, length, temperature, speed

A vector is a quantity with both magnitude and direction.

e.g. force, displacement, acceleration, velocity, momentum

Vector notation

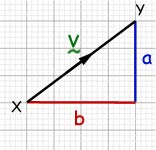
The vector from X to Y may also be represented as     V     or    

The magnitude of the vector(i.e. its number value) is expressed as:    

back to top

Inverse vectors

An inverse vector is a vector of equal magnitude to the original but in the opposite direction.

back to top

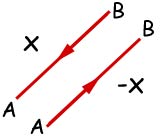
The Modulus(magnitude) of a vector

This modulus of a vector X is written l X l .

The modulus(length of the vector line) can be calculated using Pythagoras' Theorem.

This is dealt with in detail in the 'linear graphs section' here . However for completeness, the relevant formula is:

back to top

Scalar multiplication

A scalar quantity(i.e. a number) can alter the magnitude of a vector but not its direction.

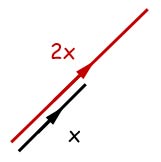
Example - In the diagram(above) the vector of magnitude X is multiplied by 2 to become magnitude 2X.

If the vector X starts at the origin and ends at the point (4,4), then the vector 2X will end at (8,8).

The scalar multiplication can be represented by column vectors:

back to top

The Triangle Law (Vector addition)

When adding vectors, remember they must run in the direction of the arrows(i.e head to tail).

A vector running against the arrowed direction is the resultant vector.

That is, the one vector that would have the same effect as the others added together.

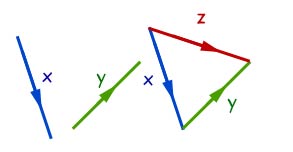
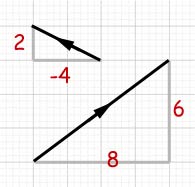
Example

A and B are vectors, as shown below. Find the magnitude of their resultant X.

First we must find the resultant vector. This is done by adding the column matrices

representing the vectors.

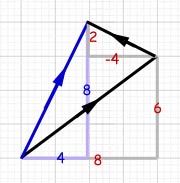
The magnitude of the resultant is given using Pythagoras' Theorem:

back to top

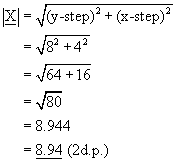
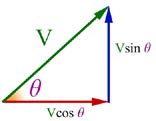
Components

A single vector can be represented by two components set at 90 deg. to eachother.

This arrangement is very useful in solving 'real world' problems.

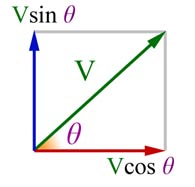
Looking at the right angled triangle below, you can see where this came from.

back to top

Unit vectors

A unit vector has unit length (1).

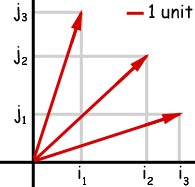
the x-axis coordinate is i and the y-axis coordinate is j

Example of a vector in terms of unit vectors : 5i + 2 j would be at coordinates (5 , 2).

Unit vector addition (& subtraction):

In turn add i terms and then add j terms.

example:

5 i + 2 j  plus  2 i + 5 j =  7 i + 7 j

in vector terms this can be expressed as:

back to top