Home >> Algebra - Linear Graphs
The equation of a straight line
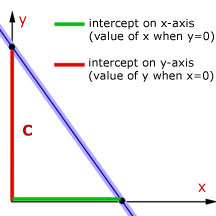
This is given the form y=mx+c, where 'm' is the gradient of the graph and 'c' is the intercept on the y-axis(i.e. when x=0).
The gradient(m)of a line is the ratio of the 'y-step' to the 'x-step' from a consideration of two points on the line.
![]()
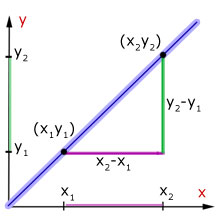
The intercept - c is the value of y when x=0. The other intercept(the value of x when y=0) is not used directly.
Since the equation of a straight line is y=mx+c, just looking at the equation is enough to give the gradient and the intercept on the y-axis.
m is the number infront of the x.
c is the number after the x term.
Example #1 Complete the table:
equation |
gradient |
intercept on y-axis |
| y = x - 3 |
+1 |
-3 |
y = -3x + 4 |
-3 |
+4 |
| y = 0.5x - 5 |
+0.5 |
-5 |
| y + x = 1 |
-1 |
+1 |
| x - y = 2 |
+1 |
-2 |
Example #2 Write down the equation of the straight line that goes through the points (2,1) and (5,7).
![]()
Putting into the equation one set of xy values(2,1),
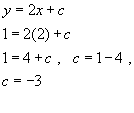
hence the equation is:
![]()
Parallel & perpendicular lines
All lines with the same gradient are parallel. However, remember in each case the intercept with the x and y axis will be different.
Examples of parallel lines - note the value of 'c' in each case.
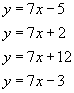
When two straight lines intersect at 90 degrees to eachother(i.e. are perpendicular), the product of their gradients is -1
Example Complete the table of gradients of lines perpendicular to eachother.
line #1 gradient |
line #2 gradient |
1 |
-1 |
-2 |
0.5 |
3 |
-0.333 |
-4 |
0.25 |
5 |
-0.2 |
The length of a line This is calculated using Pythagoras' Theorem.
The line between the two points is the hypotenuse of a right angled triangle.
Draw horizontal and vertical lines from the points.
Work out the lengths of the adjacent sides as you would to calculate gradient.
Then use Pythagoras to calculate the hypotenuse.
Example Find the length of the line joining the points (1,2) and (3,5).
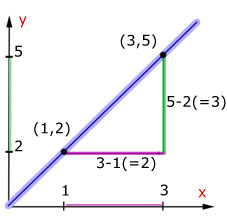
![]()
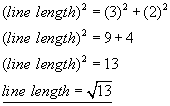
The mid-point of a line - This is simply the average of the x-coordinate and the average of the y-coordinate.
Example - if we take the two points from the last example, (1,2) (3,5), the mid point is:
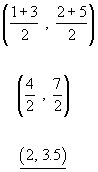
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
