Direct proportion - If y is proportional to x, this can be expressed as:

where k is 'the constant of proportionality'

A very useful equation can be obtained if we consider two sets of values of x and y.

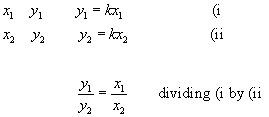
There are 4 values here. Questions on direct proportion will give you 3 of these values and you will be required to work out the 4th.

Example #1 - A car travels 135 miles on 15 litres of petrol. How many miles will the car travel if it uses 25 litres?

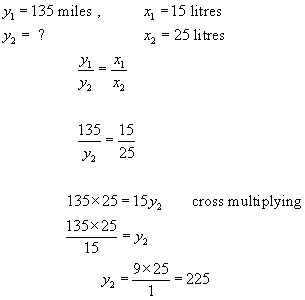
Answer: 225 miles

Example #2 - The speed v of a rocket is directly proportional to the time t it travels. After 3 seconds its speed is 150 metres per second(m/s). How long after take-off will the speed reach 550m/s ?

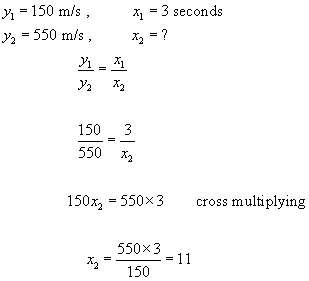
Answer: 11 seconds

back to top

Inverse proportion - If y is inversely proportional to x, this can be expressed as:

where k is 'the constant of proportionality'

Another very useful equation can be obtained if we consider two sets of values of x and y.

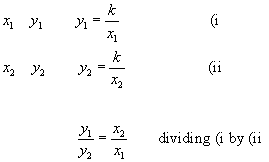
As with the equation for direct proportion, there are 4 values here. Questions on inverse proportion will give you 3 of these values and you will be required to work out the 4th.

Example - It is assumed that the value of a second-hand car is inversely proportional to its mileage. A car of value £1200 has a mileage of 50,000 miles. What will its value be when it has travelled 80,000 miles?

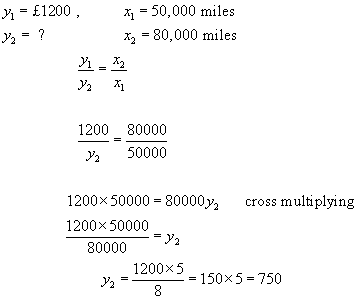
Answer: £750

back to top

Variation - This covers a number of proportionalities involving 'square', 'square root','cube root', 'cube', inverse or a combination of these.

The first thing you need to do is to write down the proportion in symbols and then as an equation. Here are some examples:

'a' is proportional to 'b' squared
'c' is inversely proportional to 'd' cubed
'e' varies as the square root of 'f'
'g' is proportional to 'h' cubed
'i' varies as the inverse of 'j' squared

In questions on variation you are usually given a pair of x,y values and a proportionality. You are given one further value of x or y, and are required to calculate the missing value.

Example - If the value of y is proportional to the square of x, and x is 4 when y is 96, what is the value of y when x is 13?

back to top

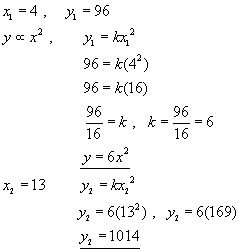
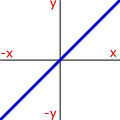
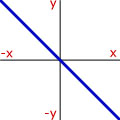
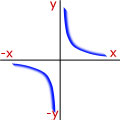
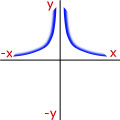
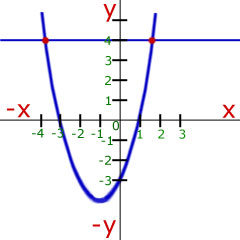
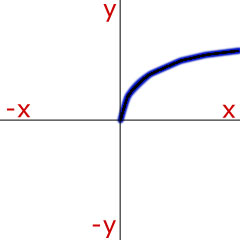
Curve Sketching - Try to remember the proportionality that matches the shape of the curve.

back to top