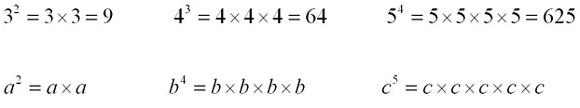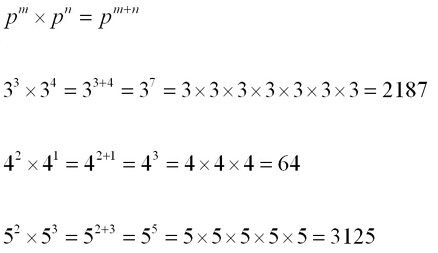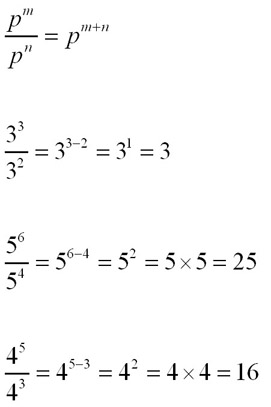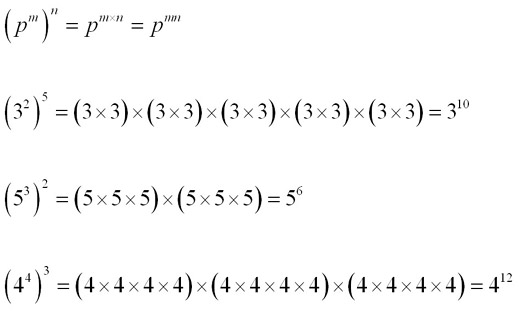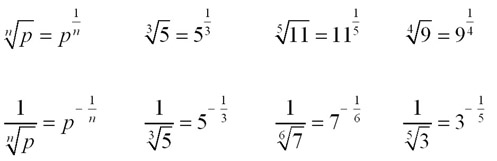Home >> Number - Powers & Roots
Index Laws : [ multiplication ] [ division ][ raised powers ][ reciprocal ][ zero ][ roots ]
Square Root The square root of a number is a number that must be squared (multiplied by itself) to give the original number.
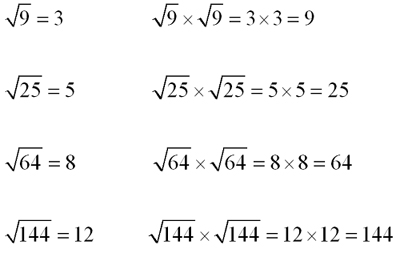
Cube Root The cube root of a number is a number that must be cubed (multiplied by itself 3 times) to give the original number.
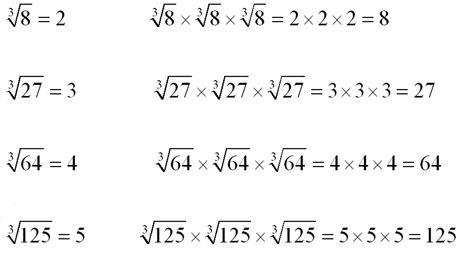
The Index Laws An 'index' (plural 'indices') is a number written in small case to the upper right of a number to indicate the number's size. An index is sometimes called the 'power' of a number.
The Index Law of Multiplication - Indices of multiplied terms are added to eachother.
The Index Law of Division - Indices of divided terms are subtracted from eachother.
The Index Law of Raised Powers - Indices of terms in brackets, raised to another power have their indices multiplied by the index outside the brackets.
The Index Law of Reciprocal Powers - The index of a reciprocal indexed quantity is multiplied by '-1' when turned upside down(inverted). Conversely, when a normal indexed quantity is inverted, its index is multiplied by '-1'.
The Index Convention for Roots - The nth root of a number is the number to the power of 1/n.
Numbers to the power of zero - All number and quantities to the power of zero have a value of '1'.
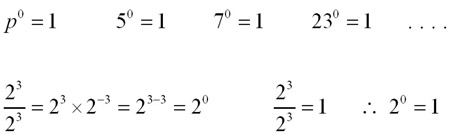
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]