Home >> Algebra - Simple Equations
| equation rules | substitution | changing the subject | creating a formula |
Simple Equations are equations with one variable only(usually denoted by 'x').
The 'Golden Rule' - whatever operations are performed, they must operate equally on both sides of the equation.
general method for solving equations:
|
a practical note:
To move a term from one side of an equation to the other, change its sign.
In effect a term of the same value but opposite in sign is added to each side of the equation. This cancels on one side giving the appearance of the original term having moved across the equation with its sign changed.
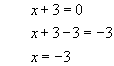
In our example -3 is added to each side of the equation. This appears to have the effect of moving the +3 across the equals sign and changing it to -3 .
Example #1
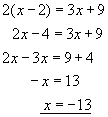
Example #2
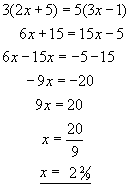
Example #3
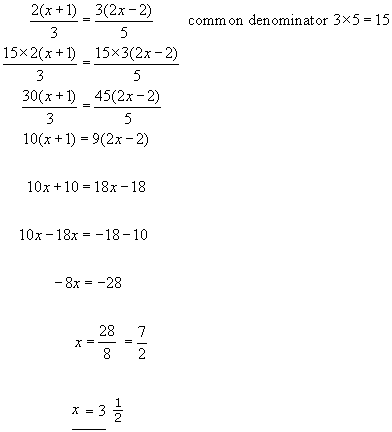
Substituting values into an equation - Simply write the equation again with the letters replaced by the numbers they represent. Use brackets to avoid arithmetic errors.
Example #1
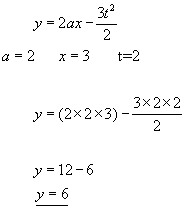
Example #2
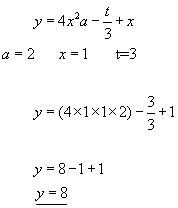
Changing the subject of an equation - Simply follow these simple rules:
|
Example #1 make 'b' the subject of the equation
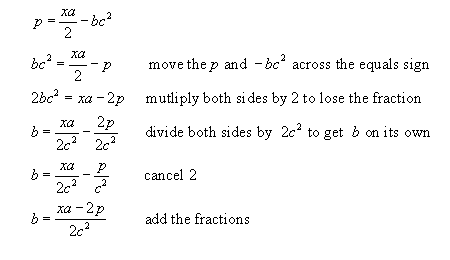
Example #2 make 'd' the subject of the equation

Example #3 make 'c' the subject of the equation
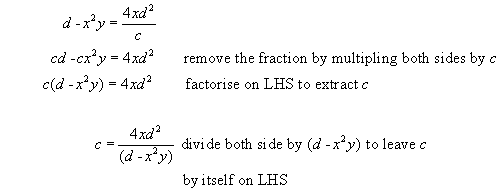
Creating a formula - Often when creating a formula some basic knowledge is required:
e.g. area of a triangle = ![]() ,
,
area rectangle = width x length etc.
Example #1 A plant of original length ![]() cm. grows at a rate of a cm. per day. If days are represented by the letter d , write an expression for the height h of the plant in cm.
cm. grows at a rate of a cm. per day. If days are represented by the letter d , write an expression for the height h of the plant in cm.
![]()
Example #2 A box has height a, length b and width c . Write an expression to represent the surface area A, of the box.
![]()
Example #3 A square box of side L contains a sphere, where the radius of the sphere is equal to half the side of the box. Write an expression for the volume in the box not taken up by the sphere.
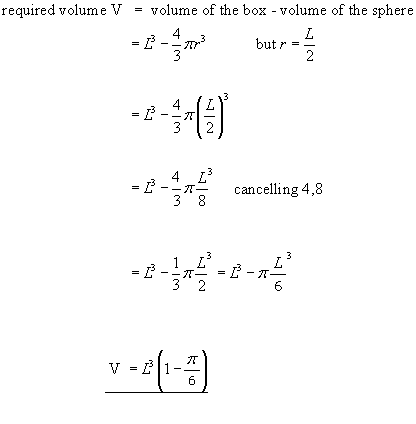
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
