[ fractions to %'s ][ %'s to fractions ][ decimals to %'s ][ %'s to decimals ]

[ % of a quantity ][ % increase ][ % decrease ][ reversed % ]

The concept of percentages depends on the principle that '1'(a whole) is represented by 100 percentage points(100%). That is, 1% =1/100 th of the whole.

Converting a fraction to a % - To do this simply multiply the fraction by 100 and cancel.

back to top

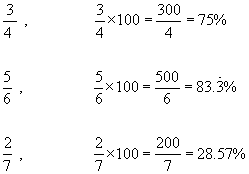
Converting a % to a fraction - For a whole number % divide by 100 and cancel. If the % has one decimal place, divide by 1000 and cancel, two decimal places, 10000, and so on.

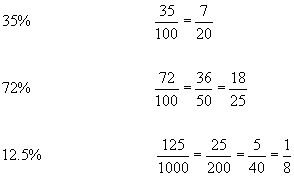
Converting a decimal to a % - Multiply the decimal number by 100.

back to top

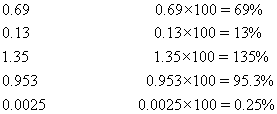
Converting a % to a decimal - Divide the decimal number by 100. This has the effect of moving the decimal point two places to the left.

back to top

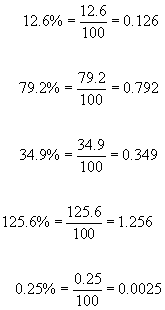
Calculating the % of a given quantity - Simply multiply by the % and divide by 100. If the % has one decimal place, divide by 1000, two places, divide by 10000 and so on.

example #1 - what is 25% of £360?

example #2 - what is 17.5% of £3000?

example #3 - what is 1.25% of £800?

back to top

Calculation of % increase - Add 100 to the % increase. Express this figure as a fraction of 100. Then multiply out with the given quantity.

example #1 - what is the final figure when a sum of £2000 is increased by 18%?

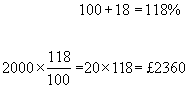
example #2 - what is the new salary if the old salary of £30,000 is increased by 5%?

example #3 - A car costing £12,000 has its price increased by 3%. What is its new price?

back to top

Calculation of % decrease - The % decrease is subtracted from 100, converted to a decimal, then multiplied by the original quantity.

example #1 - A car costing £5000 has its price reduced by 5%. What is its new price?

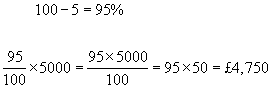
example #2 - An old house originally valued at £85,000 has its price reduced by 10%. What is its new price?

example #3 - Workers at a factory earn £12,000 per annum. If their wages are cut by 2.5%, what is their new wage?

back to top

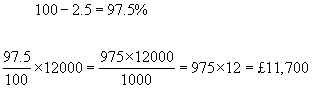
Calculation of 'reversed' percentages - The key to solving this type of problem is to work out the value of one percentage point(1%). This done by dividing the original quantity by 100 plus the % increase. Then multiply this value by 100 to obtain the original number.

example#1 - A foreign car costs 15,000 euros including 8% tax. What is the price of the car without the tax added?

value of 1 % point is :

to get the original cost we multiply the 1% point by 100

example#2 - A factory worker receives a salary of £18,000 after a 5% pay rise. What was the salary of the worker before?

value of 1 % point is :

to get the original salary we multiply the 1% point by 100

example#3 - A farmer has a flock of 1210 sheep that have increased their number by 10% over the year. How many sheep were there the year previous?

value of 1 % point is :

to get the original number of sheep we multiply the 1% point by 100

back to top