A 'straight line intersecting a straight line' is dealt within 'simultaneous equations' here

Vertical line intersecting a quadratic curve

Example     Find the point of intersection when the vertical at x=-2 meets the curve,

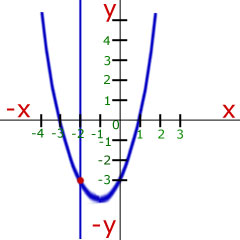
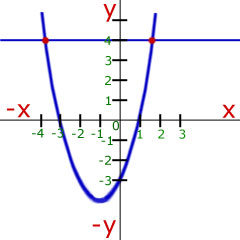
Substitute the value of x=-2 into the quadratic equation to find y.

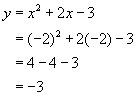
hence the point of intersection is (-2, -3)

back to top

Horizontal line intersecting a quadratic curve

Example     Find the two points of intersection when the horizontal at y=4 meets the curve,

To find the two points, put one equation equal to the other, rearrange putting zero on one side and find the roots.

The roots are complex, therefore we use the quadratic equation formula:

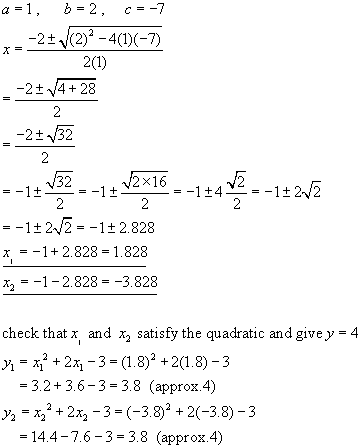
The two points of intersection are (1.828, 4) and (-3.828, 4)

N.B. the rounding of square roots makes the answers only approximate

back to top

Angled straight line intersecting a quadratic curve

Example - Find the points of intersection when the straight line with equation,

meets the curve,

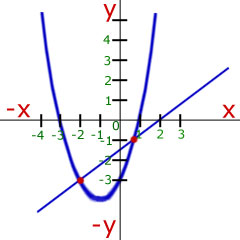
As with the horizontal line intersection , the solution is to put one equation equal to the other, rearrange, put zero on one side and find the roots.

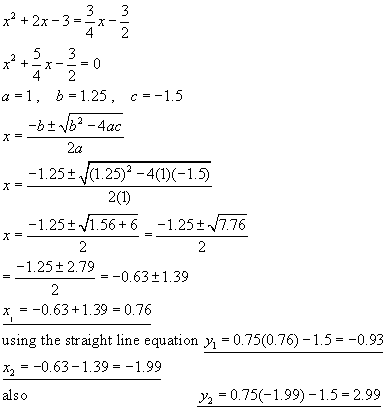
The two points of intersection are(0.76, -0.93) and (-1.99, 2.99)

back to top

Straight line intersecting a circle

Example - Find the points of intersection when the straight line with equation,

meets the circle with equation,

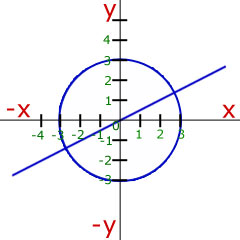
The solution is to take the y-value from the straight line equation and put it into the y-value of the circle equation. Then solve for x.

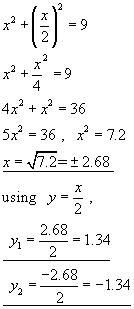
The two points of intersection are(2.68, 1.34) and (-2.68, -1.34)

back to top