Home >> Algebra - Proportion
Direct proportion - If y is proportional to x, this can be expressed as:
![]()
![]()
where k is 'the constant of proportionality'
A very useful equation can be obtained if we consider two sets of values of x and y.
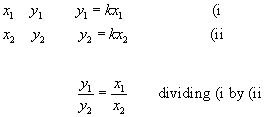
There are 4 values here. Questions on direct proportion will give you 3 of these values and you will be required to work out the 4th.
Example #1 - A car travels 135 miles on 15 litres of petrol. How many miles will the car travel if it uses 25 litres?

Answer: 225 miles
Example #2 - The speed v of a rocket is directly proportional to the time t it travels. After 3 seconds its speed is 150 metres per second(m/s). How long after take-off will the speed reach 550m/s ?

Answer: 11 seconds
Inverse proportion - If y is inversely proportional to x, this can be expressed as:
![]()
![]()
where k is 'the constant of proportionality'
Another very useful equation can be obtained if we consider two sets of values of x and y.
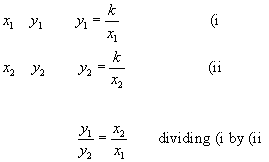
As with the equation for direct proportion, there are 4 values here. Questions on inverse proportion will give you 3 of these values and you will be required to work out the 4th.
Example - It is assumed that the value of a second-hand car is inversely proportional to its mileage. A car of value £1200 has a mileage of 50,000 miles. What will its value be when it has travelled 80,000 miles?
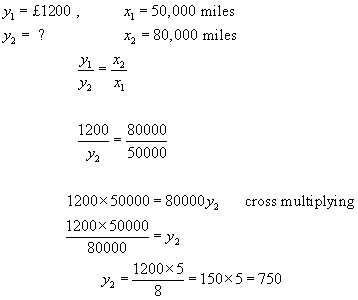
Answer: £750
Variation - This covers a number of proportionalities involving 'square', 'square root','cube root', 'cube', inverse or a combination of these.
The first thing you need to do is to write down the proportion in symbols and then as an equation. Here are some examples:
'a' is proportional to 'b' squared |
||
'c' is inversely proportional to 'd' cubed |
||
'e' varies as the square root of 'f' |
||
'g' is proportional to 'h' cubed |
||
'i' varies as the inverse of 'j' squared |
In questions on variation you are usually given a pair of x,y values and a proportionality. You are given one further value of x or y, and are required to calculate the missing value.
|
Example - If the value of y is proportional to the square of x, and x is 4 when y is 96, what is the value of y when x is 13?
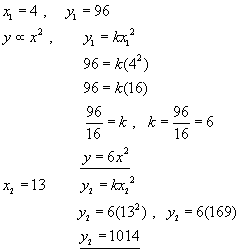
Curve Sketching - Try to remember the proportionality that matches the shape of the curve.
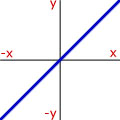 |
|
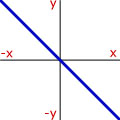 |
|
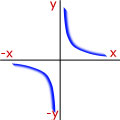 |
|
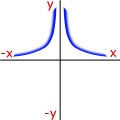 |
|
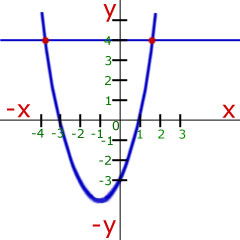 |
|
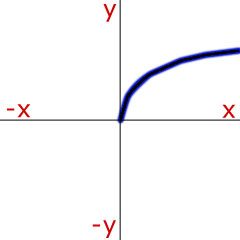 |
|
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
